Disk Vibrations

tags: Fortran programmingnumerical modellingfourier transformtravelling wave

One of the fundamental phenomena considered while designing rotating disks are vibrations which may cause high cycle fatigue and subsequently release significant amount of Energy. For prime reliable parts such as aviation engine disks it may result in uncontained engine failure which is a significant safety concern. While in most of the cases resonance can be avoided using simple criteria the nature of resonant response is not so simple to understand for axisymmetric structures like disks. Goal of the following article is to visually explain the origin of resonance occurring in rotating circular plates.

Basic tool for studying disk dynamics is Kirchhoff-Love plate theory which describes dynamic behavior by the following differential equation expressed in polar coordinates [1]:

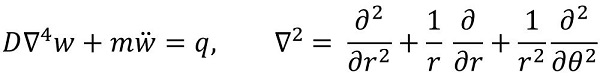
where w is plate transverse displacement, q is the transverse load per unit area and D is the bending stiffness. In order to solve this equation for given boundary conditions finite difference method was used which replaces partial differential derivatives with algebraic formulas applied in discrete space domain [2]. Euler method was used to integrate the equation in time domain [3]. Fortran programming language was used to efficiently implement algorithms and postprocess the results. Analyzed would be thin disk fixed at inner diameter excited by different loads applied to outside diameter.

Fundamental concept in vibration theory is that for the resonance to occur excitation frequency shall be equal to one of the system natural frequencies. For circular plate, each resonant response associated with particular natural frequency (mode shape) is often pictured as back and forth deflection:

Fig 1. Disk ND5 resonant response at 820Hz.

This is the quasi-static resonant response due to stationary harmonic excitation applied to the Edge of numerical model. Such response is often called Nodal Diameter 5 (ND5) since there are five lines with no deflections at any moment in time called nodal lines. In order to examine the origin of such response its worth looking how does it develop from t=0.0s

Fig 2. ND5 transient response due to harmonic stationary excitation.

Local excitation creates two waves travelling around disk circumference in opposite directions. These waves eventually meet at the other end of the disk, travel further and interfere with each other. This results in standing resonance wave which occurs when harmonic excitation frequency match one of the natural frequencies. Response is amplified as Energy is delivered to the system since excitation and deflection velocity directions match at any moment in time.

To further analyze circular plate responses lets consider sudden initial disturbance at one end of disk (note that time scale is significantly smaller):

Fig 3. Transient response due to sudden disturbance (ping test).

Local, sudden disturbance generates set of waves travelling outwards the origin of disturbance. Each wave has different speed and wavelength. Shorter waves travel faster the longer ones. As shown on previous example waves eventually meet and interfere with each other. Such case resembles the ping test which is often performed to examine natural frequencies of the system as is generates all possible waves at once. Similar effect is visible on the following slow motion video (only long waves are visible):

Fig 4. Example of thin disk response due to sudden local disturbance [4].

In turbomachinery design disks resonance may be driven by non-uniform static pressure field which, due to disk angular velocity, seems to rotate relative to it eg. Bleed port in casing which generates pressure drop. As disk rotates it experiences a constant magnitude pressure disturbance travelling around its circumference. It was shown that local disturbance generates set of waves travelling with different speeds around the disk. Let’s apply static load which would follow one of these waves:

Fig. 5. Response to constant travelling load.

There is no angular velocity applied to the disk itself but the ND5 response occurs in form of a wave travelling around the disk. The load itself is not harmonic either however the resonance occurs anyway. Often excitation is periodical in tangential direction. When shape of excitation (eg. Pressure distribution formed by multiple ventholes in static structure) and disk speed match the mode shape (nodal diameter) and associated wave propagation speed strong resonance would occur:

Fig. 6. Strong resonance for ND5.

When disk rotates the wave travels relative to it and when resonance occurs disk speed matches the wave speed. As a result wave would appear stationary to stationary observer in spite of the fact that disk is spinning. It can be clearly seen on the following video (the disk fails just before wave and disk speed match what clearly shown how strong that phenomenon is):

Fig. 7 Example of wave speed coincidence in 170 000fps [5]

It shows that constant force travelling around the disk can excite ND5. In order to screen which modes can be excited multiple analysis runs were performer for various RPM’s. After each analysis Fourier transform of time-displacements was done to generate frequency-speed diagram and to show possible resonant conditions:

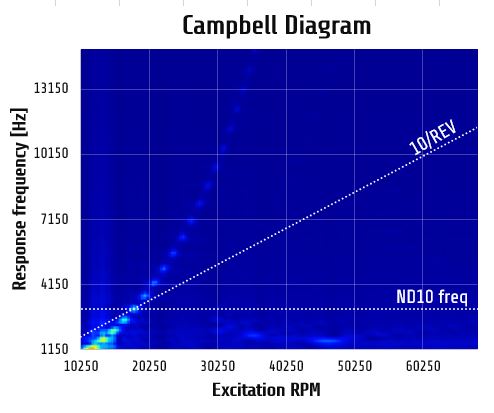
Fig 8. Frequency – speed diagram

Major resonance occurs when natural frequency of particular ND crosses with same per/rev line [1]. In example from fig 5 ND5 resonance occurs when its natural frequency 820Hz is excited with 5/rev excitation at 9840rpm (9840/60*5=820Hz) – It is called a major resonance. It means the travelling wave becomes stationary when on freq-speed diagram particular ND crosses with corresponding per/rev. Another essential conclusion arising from fig 8 is that at major resonance any static excitation acting on a spinning disk can potentially generate significant response.

Above article just scratches the Surface of disk travelling waves phenomenon but hopefully gives a good picture of the origin of resonance in such structures.